Quantum Matter

List of articles on this topic

Liquid and solid helium

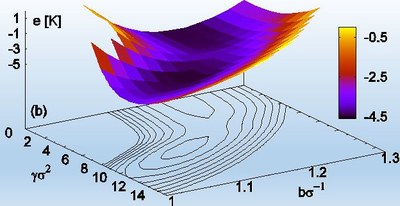
Liquid helium is a historical example of an extremely highly correlated quantum system, which is hard to describe quantitatively using perturbative methods. The He-He interaction potential is known from high-precision experiments. Its use in ab initio Quantum Monte Carlo simulations resulted in a spectacular agreement with the experimental equation of state, correlation functions, and excitation spectrum. We proposed a single wave function capable of describing both the liquid and solid phases. The figure shows the variational energy as a function of parameters. Two minima are visible, one corresponding to the liquid phase, the other to the solid one. As the density is increased, there is a phase transition from liquid to solid.

Supersolid

One of the fundamental questions of quantum physics is a possibility of a simultaneous coexistence of a crystalline order (solid) and superfluidity or long-range coherence. An observation of this "supersolid" was reported in a number of experiments with helium. Still the signal was very weak, the experimental measurements were not reproducible. The studies carried out in our group have shown that the signal observed is incompatible with zero-temperature properties of a bulk system. Adding defects (vacancies, interstitials) increases greatly the superfluid signal.

Nanostructures

Recent experimental progress in nanotechnology has permitted to controllably create structures on nanometer scales, with atoms forming some desired shape. Such structures are expected to play an important role in future technologies. The adsorption on carbon nanotubes were studied in BQMC group. Another recently created materials are graphene and graphite, both studied in our group.

Quantum electron wires

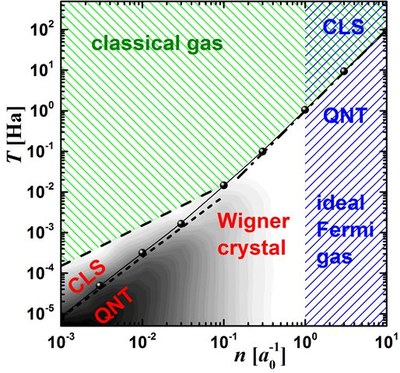
We obtain the phase diagram of a quantum electron wire. Due to the long-range nature of the Coulomb interaction, the Wigner crystal is formed at low densities. As the density is decreased, there is a phase transition between a classical gas and a classical Wigner crystal. At even lower temperatures, the Wigner crystal becomes quantum. By increasing the density there is a crossover from it to a quantum ideal Fermi gas. As the temperature is increased the quantum gas converts into a classical thermal gas.
For low temperatures, we predict an unusual double transition as the density is increased, involving gas – Wigner crystal – quantum Fermi gas transition.

One-dimensional Bose gas in an optical lattice

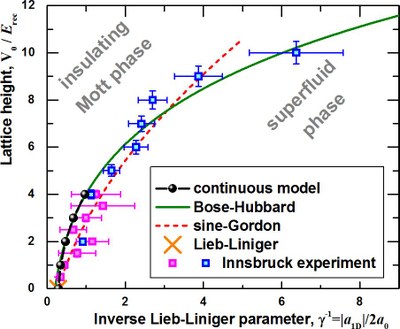
We investigate the properties of an interacting Bose gas in an optical lattice starting directly from a continuous-space description. There is a superfluid- insulator phase transition as the strengths of interactions and of the optical lattice are varied. For deep lattices, we find agreement with a discrete Bose-Hubbard model, which is one of the fundamental models in condensed matter physics. We establish the limits of applicability of the Bose-Hubbard model. We find a good agreement with the position of the phase transition measured experimentally.

Dipolar systems

Dipolar interactions attract a lot of attention because of their strong anisotropic character. In the field of ultracold dilute atoms there is an additional interest due to the long range of dipolar interactions, compared to short-ranged s-wave scattering. The properties of dipolar systems were addressed in zero-temperature quantum regime, and at a finite temperature.

An ultracold dilute Bose gas forms a condensate, described by a macroscopic wave function with a certain phase. If we consider two layers with dipoles, separated by a large distance, there will be two condensates with independent phases. For very small separation between layers, dipoles from different layers form dimers (molecules). Being again bosons, dimers form a Bose-Einstein condensate with a single phase, effectively locking the phase between different layers. This transition between two Bose condensates into a single one is an unusual phenomena for which we provide a detailed description.

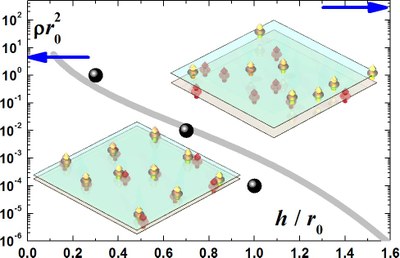
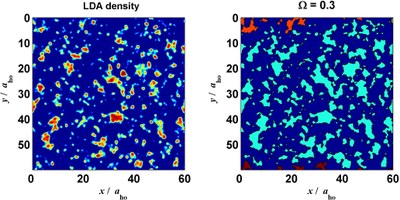
Disorder

We study how the presence of disorder affects a weakly-interacting Bose gas. As the strength of the speckle disorder is increased, the superfluid and zero-momentum fractions get depleted, finally resulting in a localized normal state. We find that in a vast regime of densities the system properties are correctly reproduced by Gross-Pitaevskii equation, as is obtained in a comparison with Diffusion Monte Carlo results. Localization is analyzed as a percolation problem. The case of a weak disorder and weak interactions is studied perturbatively within Bogoliubov approach.

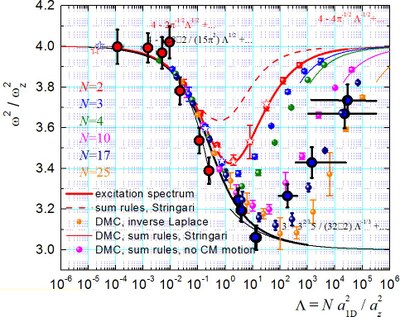
Frequency of collective oscillations in a one-dimensional Bose gas

A collective “breathing” mode can be excited in a trapped system by suddenly changing the trapping confinement. The frequency of the resulting oscillations probes the interactions between the particles. It was predicted and experimentally observed that the square of the frequency changes from 4 to 3 as the interaction strength is changed from strong to weak. An unexplained result was that the square of the frequency goes back to 4 for very weak interactions. We were able to successfully reproduce this reentrant behavior, for which we provide an explanation in terms of the finite-size effects.