Ferran Mazzanti Homepage
Here you'll find information about my activities at the university and out of it.
You can always reach me by e-mail at Ferran.Mazzanti![]() upc.edu
upc.edu
My main fields of research are Condensed Matter and Quantum Many-Body physics, although I also work on a very specific kind on neural networks called Boltzmann machines. More specifically my preferred topics are:
Liquid Helium
 |
Helium is the lightest of the noble gases and due to its low mass shows amazing quantum properties that can be observed at amacroscopic level, such as Bose-Einstein Condensation and Superfluidity.Besides, the interatomic potential between pairs of Helium atoms is fairly well known and one can easily calculate static and (some) dynamic properties at zero and low temeratures using either variational or Monte carlo techniques.Superfluid Helium was discovered in the beginning of the 20th century and has since then attracted the interest of many nowadays well honored physicists. Despite Helium has been studied for more than fifty years, there are still some aspects not very well understood such as the exact relation between a Bose condensate and superfluidity.Homogeneous and inhomogeneous Helium, 1D, 2D or 3D Helium, liquid, solid, pure or in mixtures... what's your favourie flavour? |
Bose-Einstein condensation
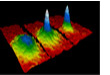 |
Bose-Einstein Condensation (BEC) is perhaps the most up-to-the-date field of interest in many-body physics. it was as late as 1995 when Eric Cornell and Carl Wieman in Boulder, Colorado, achieved the first neat realization of a Bose condensate conatining almost 100% of particles on it. Up to that date only indirect meaurements of Bose condensates where performed, as for instance the extra strength in the peak of the dynamic structure function of 4He at high momentum transfer. Many things have happened since 1995 and nowadays experimental physicists are able to do wonders with these magnetically trapped condensates, and the number of atoms confined is increasing every day. |
Dinyamic Structure Function of Quantum Fluids
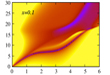 |
One of my main interests regarding quantum fluids is the description of their dynamic properties. Ground state quantities are more or less known as powerful tools such as the Monte Carlo or the Variational methods have proven to succesfully describe these properties. Now the challenge is to describe excitations. Well to tell the truth muchinformation regarding elementary excitations and collective modes in quantum liquids have been gathered, and powerful methods based on variational models have been succesfully applied to describe S(q,w) at low and high momentum transfer. Still in quantum liquids are less understood than groundtstae properties and there is room for more work. The dynamic structure function is the maximum information about the dynamics of the system one can get from an inelastic neutron scattering experiment, so that is a good starting point. |
Path Integral and Monte Carlo Simulations
 |
Since the beginning of 2006 I started to work on simulation methods at the UPC. Monte Carlo and Path Integral monte Carlo are perhapshe most prominent tools in the study of quantum systems right now. Aside from statistical errors, these methods solve exactly the many-body problem. Once again I'll be using them to study mostly static properties of quantum fluids like Helium, Bose-Einstein condensates and/or weakly interacting Bose and fermi systems. I am by no means an expert on that, but that's going to be for the sure the main tool I'll be using in my research on quantum fluids for the next years. Right now that means learining and testing algorithms, but taking into account the team of people I work with, that's going to be a rewarding activity for sure. |
Boltzmann Machines
 |
Before I started to work at the Universitat politècnica de catalunya I was an associate professor at Enginyeria i Arquitectura La Salle from the Universitat Ramon Llull. People there is much more interested in engineering that in physics, so I decided to do some research in a filed that could interest them and me. Neural networks was the perfect field since many techniques commen in statistical mechanics are used in the analysis of the computational capabilities of neural networks. Boltzmann machines caught my interest due to its unique property of learning probability distributions. What began as sort of a game soon became a promising field of activity where new learning techniques were developped and tested against the performance of classical learning algorithms. |
Share: